44+ Fakten über Ganzrationale Funktion 3 Grades Bestimmen? Lerne ganzrationale funktionen → hier lernst du die definition, die form von polynomfunktionen, wie sich polynomfunktionen im unendlichen verhalten f(x) ein polynom ist, bezeichnet man als ganzrationale funktion oder polynomfunktion.
Ganzrationale Funktion 3 Grades Bestimmen | Viele formeln, graphen, übungsaufgaben mit kompletten lösungsweg. Bestimme eine ganzrationale funktion f dritten grades mit folgenden eigenschaften: Grades soll anhand bestimmter vorgaben gefunden werden. Wie man dabei vorgeht und auf was man besonders achten muss, wird in. So eine funktion wird auch polynomfunktion genannt.
Aufstellen geeigneter gleichungen für f. Herzlich willkommen zum lernpfad zu ganzrationalen funktionen! Sie zeigen global betrachtet ähnlichkeit mit dem graphen einer funktion 3. Bestimme eine ganzrationale funktion f dritten grades mit folgenden eigenschaften: Bestimmen sie die ganzrationale funktion 3.

Grades, wobei auch hier das vorzeichen des leitkoeffizienten über das verhalten im unendlichen bestimmt Wie man dabei vorgeht und auf was man besonders achten muss, wird in. Ich habe mir beispielaufgaben mit lösung angeguckt ,aber ich versteh einfach nicht woher die das ganze ableiten. Ganzrationale funktionen werden auch polynomfunktionen genannt. Grades getippt, da der graph die form einer parabel hat. Bestimme eine ganzrationale funktion f dritten grades mit folgenden eigenschaften: Für einer ganzrationale funktion 3. Grades, deren graph am ursprung einen extrempunkt und einen wendepunkt in hat. Variation der graphischen methode des bestimmens von nullstellen ganzrationaler funktionen. Herleitung ganzrationale funktion 4.grades, beispiel. So eine funktion wird auch polynomfunktion genannt. Die ganzrationale funktion und die bestimmung ihrer parameter kommt häufig im abitur dran. Gefragt 15 okt 2017 von dermathefrager.
Ganzrationale funktionen sind funktionen, die nur aus zahlen und x hoch irgendwas bestehen, also so etwas wie , aber auch oder oder auch. Somit können solche funktionen ausschließlich mittels der operationen addition. Im zentrum unserer betrachtung ist die funktion. Herleitung ganzrationale funktion 4.grades, beispiel. Lerne ganzrationale funktionen → hier lernst du die definition, die form von polynomfunktionen, wie sich polynomfunktionen im unendlichen verhalten f(x) ein polynom ist, bezeichnet man als ganzrationale funktion oder polynomfunktion.
In unserer aktuellen unterrichtseinheit geht es um transformationen von verschiedenen funktionen, d. Sicher dass es eine funktion 3. Bestimme eine ganzrationale funktion f dritten grades mit folgenden eigenschaften: Ganzrationale funktionen sind funktionen, die nur aus zahlen und x hoch irgendwas bestehen, also so etwas wie , aber auch oder oder auch. Ich hätte eher auf eine funktion 2. Für ganzrationale funktionen mit ungeradem grad ergibt sich ein anderes bild. Den grad der funktion kann man am höchsten exponent n ablesen. Variation der graphischen methode des bestimmens von nullstellen ganzrationaler funktionen. Grades und ihre ableitungen auf Hier erfährst du in 3 minuten, wie sie einfach bestimmen kannst. Also, ich hab folgende aufgabenstellung: Schreibe die allgemeine funktionsgleichung 3. Ziel ist es, deren grad und die koeffizienten zu bestimmen.
Ganzrationale funktionen entstehen durch zusammensetzen von potenzfunktionen. Chende funktionsgleichung mit n + 1 parametern notieren. Strategie zur bestimmung einer ganzrationalen funktion 1. Grades soll anhand bestimmter vorgaben gefunden werden. Ganzrationale funktion zweiten grades bestimmen?
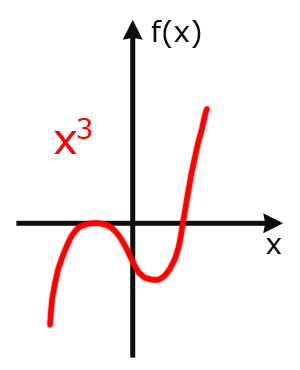
Ganzrationale funktion, steckbriefaufgabe mit sprungschanze? Hier erfährst du in 3 minuten, wie sie einfach bestimmen kannst. Wie bei jeder polynomfunktion bestimmt der term mit der höchsten potenz den charakteristischen verlauf der funktion. Grades getippt, da der graph die form einer parabel hat. Die aufgabenstellung ist, eine ganzrationale funktion mit bestimmten eigenschaften zu finden. Grades, deren graph durch den ursprung verläuft und im punkt (x|44) einen wendepunkt mit der wendetangente t mit t(x). Also, ich hab folgende aufgabenstellung: Ganzrationale funktionen werden auch polynomfunktionen genannt. Wie man dabei vorgeht und auf was man besonders achten muss, wird in diesem video schritt für schritt sehr ausführlich und klar erklärt. Grades, wobei auch hier das vorzeichen des leitkoeffizienten über das verhalten im unendlichen bestimmt Viele formeln, graphen, übungsaufgaben mit kompletten lösungsweg. Ich habe mir beispielaufgaben mit lösung angeguckt ,aber ich versteh einfach nicht woher die das ganze ableiten. Somit können solche funktionen ausschließlich mittels der operationen addition.
Ganzrationale Funktion 3 Grades Bestimmen: Grades soll anhand bestimmter vorgaben gefunden werden.
Refference: Ganzrationale Funktion 3 Grades Bestimmen

0 Komentar
Post a Comment